Basic Setup
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
from numpy.random import normal
T = 2.0
n = 100
dt = T / n
First test: solving a simple equation
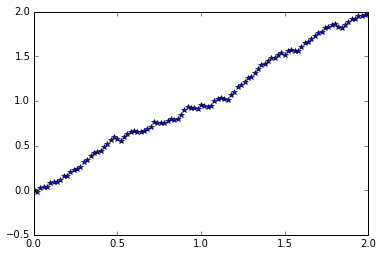
x = np.zeros(n + 1)
for i in xrange(n):
x[i + 1] = x[i] + dt + normal(scale = dt)
t = np.linspace(0, T, n + 1)
plt.plot(t, x, '*')
[<matplotlib.lines.Line2D at 0x3a55b10>]
Stochastic maltus model
Problem parameters
r = 1
c = 1
x0 = 1
t = np.linspace(0, T, n + 1)
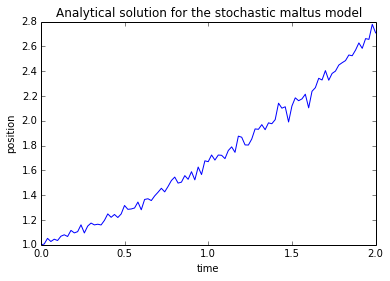
Analytic solution
factor = r - c**2 / 2.0
x = np.ones(n + 1)
w = normal(scale=dt, size=n + 1)
w[0] = 0
x = x0 * np.exp(factor * t + c * w)
plt.plot(t, x)
plt.title('Analytical solution for the stochastic maltus model')
plt.xlabel('time')
plt.ylabel('position')
<matplotlib.text.Text at 0x48dd910>
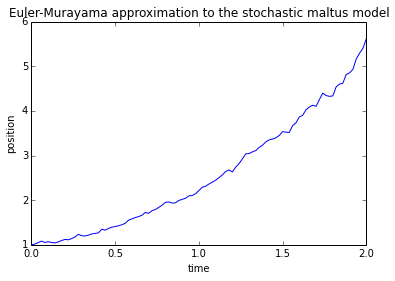
Euler-Murayama approximation
x2 = np.zeros(n + 1)
x2[0] = x0
for i in xrange(n):
xi = x2[i]
x2[i + 1] = xi + r * xi * dt + c * xi * normal(scale = dt)
plt.plot(t, x2)
plt.title('Euler-Murayama approximation to the stochastic maltus model')
plt.xlabel('time')
plt.ylabel('position')
<matplotlib.text.Text at 0x4dd5b50>
Milstein method
x3 = np.zeros(n + 1)
x3[0] = x0
for i in xrange(n):
xi = x3[i]
wi = normal(scale = dt)
x3[i + 1] = xi + r * xi * dt + c * xi * wi + 0.5 * c * xi * c * (wi**2 - dt)
plt.plot(t, x3)
plt.title('Milstein method to approximate the stochastic maltus model')
plt.xlabel('time')
plt.ylabel('position')
<matplotlib.text.Text at 0x4dcc590>
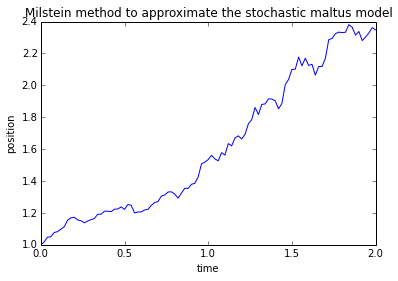
Qualitative comparison
plt.plot(t, x, t, x2, t, x3)
plt.title('Qualitative comparison of the three methods')
plt.xlabel('time')
plt.ylabel('position')
plt.legend(('Analytic', 'Euler-Murayama', 'Milstein'), loc='upper left')
plt.grid()
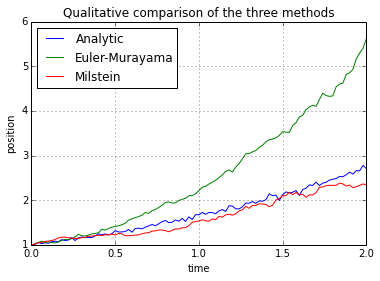
As it was expected, euler’s method is more prone to error than Milstein’s correction. It remains to make a comparison of results for different values of the parameters. It is not expected any important difference in the results if varying initial conditions
Appendix: Routines for solving sde
It is straightforward to write routines for solving stochastic equations with Euler-Murayama’s and Milstein’s methods. For later, convenience, they are written here.
def emurayama(T, timesteps, x0, alpha, beta):
'''
x = emurayama(T, timesteps, x0, alpha, beta)
solves the stochastic differential equation
dx = alpha * dt + beta * dw
x(0) = x0
with Euler-Murayama method.
input:
T = Final time.
timesteps = Number of timesteps to use.
x0 = initial condition.
alpha, beta = equation parameters. Must be functions like this:
x = alpha(xi, ti),
i.e. its input must be two floating point numbers and must return another floating point.
(No vectorization, due to the recursive definition of the algorithm)
returns:
array of lenght timesteps + 1 with the result.
'''
x = np.zeros(timesteps + 1)
x[0] = x0
ti = 0.0
dt = float(T) / timesteps
for i in xrange(timesteps):
xi = x[i]
ti += dt
x[i + 1] = xi + alpha(xi, ti) * dt + beta(xi, ti) * normal(scale = dt)
return x
def milstein(T, timesteps, x0, alpha, beta, diff_beta):
'''
x = milstein(T, timesteps, x0, alpha, beta)
solves the stochastic differential equation
dx = alpha * dt + beta * dw
x(0) = x0
with Milstein's method.
input:
T = Final time.
timesteps = Number of timesteps to use.
x0 = initial condition.
alpha, beta = equation parameters. Must be functions like this:
x = alpha(xi, ti),
i.e. its input must be two floating point numbers and must return another floating point.
(No vectorization, due to the recursive definition of the algorithm)
diff_beta = partial derivative of beta, respect to x.
returns:
array of lenght timesteps + 1 with the result.
'''
x = np.zeros(timesteps + 1)
x[0] = x0
ti = 0.0
dt = float(T) / timesteps
for i in xrange(timesteps):
xi = x[i]
ti += dt
wi = normal(scale = dt)
x[i + 1] = xi + alpha(xi, ti) * dt + beta(xi, ti) * wi + 0.5 * beta(xi, ti) * diff_beta(xi, ti) * (wi**2 - dt)
return x