Definition

A set of points in $\mathbb{R}^n$, $\{v_0, \ldots, v_m\}$ is in general position (this name is not standard) if the vectors $\{v_m - v_0, \ldots, v_1 - v_0\}$ are linearly independent.

Theroem

If the set of vectors $\{v_0, \ldots, v_m\}$ is in general position, then after rearranging the set, it is yet a set in general position.

In other words, no matter what vector $v_k$ is fixed, the vectors $v_r - v_k$ are linearly independent, provided we exclude $v_k - v_k$.

A set of vectors in general position

Proof

excercise

Definition

A subset $S \subset \mathbb{R}^n$ is convex if for every $x, y \in S$, the linear segment joining the points, $t\,x + (1- t)\,y$, $0 \leq t \leq 1$ is also contained in $S$.

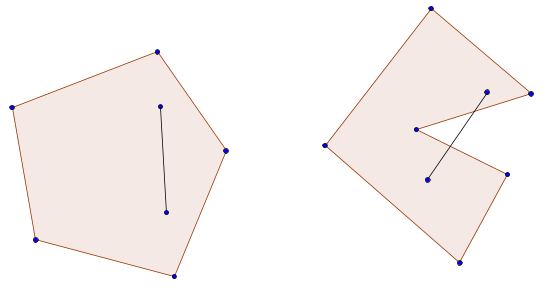
A convex and a non-convex set

Definition

Given the points $\{v_0, \ldots, v_n\}$ in general position, the n-simplex $\Delta(v_0, \ldots, v_n)$ generated by the vectors is the set

$\left\{\sum_{i=0}^n s_i\,v_i\mid s_0 + \cdots + s_n = 1 \right\}$

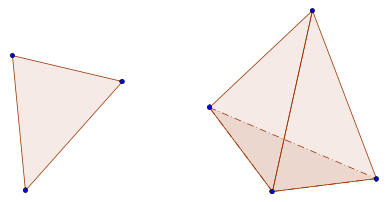
two and three-simplices in the space.

Theorem

An n-simplex set is convex.

Proof

Let $x, y \in \Delta(v_0, \ldots, v_n)$, and $0 < t < 1$. There exist constants $\lambda_i$, $\mu_j$ such that

and

Therefore,

and

Given that $x$, $y$ are points in the simplex, $\sum\lambda_i = 1$, $\sum\mu_i = 1$. The theorem follows.

Definition

Fix a vertex $v_k$ in the simplex $\Delta(v_0,\ldots, v_n)$, the $\Delta^k$ face of the simplex is the n - 1 simplex $\Delta(v_0, \ldots, \hat{v_k}, \ldots, v_n)$, obtained by supressing the vertex $v_k$.

Theory of the simplex method

Let $f:\mathbb{R}^n \to \mathbb{R}$ be a linear function. Our main objective is to maximize $f$ in a simplex domain.

Theorem

If $f$ is linear and $\Delta$ is a n-simplex in $\mathbb{R}^n$, the restriction $f|_\Delta$ reaches its maximum at a vertex.

Proof

Let $v_0, \ldots, v_n$ be the vertices of $\Delta$.

Since $f$ is linear, it is continous. Note that $\Delta$ is compact. Therefore, there is a maximum value for $f$ in $\Delta$. If $f$ is the zero function, the theorem is trivial. On the other hand, if $f$ is not null, its restriction to the space generated by the vectors $v_n - v_0, \ldots, v_1 - v_0$ is a linear function, and therefore the restriction of $f$ to $\Delta$ is an afin function (a composition of a linear function and a translation). Note that its maximum value can not lie in the interior of the simplex, since $\nabla f \neq 0$.

We will use induction in the simplex dimension. Consider a 1 simplex $\Delta(v_0, v_1)$, since its border points are $v_0$ and $v_1$ the theorem follows. Consider the general case,

Let $\Delta^k$ be the n - 1 face of the simplex where $f$ attains its maximum. Since $\Delta^k$ is itself a simplex, with one dimension less, the maximum must be attained in a vertex.

Given an optimization problem with a linear function, the previous theorem implies that to solve it, one must search for the maximum of $f$ in the finite set of vertices.

Suppose we use this algorithm in the following way: Given a linear optimization problem, constrained to a $\Delta$ simplex, we must solve it restricted to a certain maximum amount of time. As iterating is easier to represent than time measuring in a discrete problem, suppose the restriction is on the number of iterations. Therefore, we decide to procceed as follows: On each iteration we select randomly a vertex in the simplex, with uniform probability distribution. What would be the expectation value on the number of iterations needed to find the max?